“匀变速” 是物理学中描述物体运动状态的重要概念,主要用于研究物体速度随时间的变化规律,核心特征是速度的变化率(加速度)保持恒定。以下从定义、分类、规律及应用等方面详细解析:
一、核心定义
物体在运动过程中,加速度(速度对时间的变化率)不随时间改变,即加速度的大小和方向均保持恒定,这种运动状态称为 “匀变速运动”。
数学表达:加速度
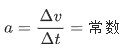
(Δv 为速度变化量,Δt 为时间变化量)。
关键:速度可以增大、减小或改变方向,但速度的 “变化快慢” 始终不变。
二、常见分类(按运动轨迹划分)
1. 匀变速直线运动
定义:物体沿直线运动,且加速度恒定(与速度方向共线)。
细分类型:
匀加速直线运动:加速度与速度方向相同,速度随时间均匀增大(如自由下落的物体,忽略空气阻力时加速度为重力加速度g)。
匀减速直线运动:加速度与速度方向相反,速度随时间均匀减小(如刹车时的汽车,加速度与运动方向相反)。
基本公式(以初速度 v 0、加速度 a 为例):
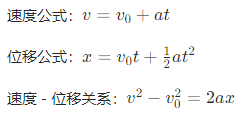
2. 匀变速曲线运动
定义:物体运动轨迹为曲线,且加速度恒定(加速度与速度方向不共线,导致速度方向不断变化)。
典型案例:
平抛运动:物体以水平初速度抛出,仅受重力(加速度 g 竖直向下),轨迹为抛物线。
斜抛运动:物体以斜向初速度抛出,仅受重力,轨迹为对称抛物线(上升阶段减速,下降阶段加速,加速度始终竖直向下)。
特点:加速度恒定,但速度方向随轨迹切线方向变化,因此是 “变速曲线运动”,但因加速度不变,仍属于 “匀变速” 范畴。
三、与 “非匀变速运动” 的区别
对比项 匀变速运动 非匀变速运动
加速度 大小和方向均不变 大小或方向随时间变化
速度变化规律 速度均匀变化(Δv 与 Δt 成正比) 速度变化不均匀
举例 自由落体、平抛运动 圆周运动(加速度方向时刻指向圆心)、汽车急加速(加速度增大)
四、物理意义与应用
基础研究价值:匀变速运动是研究复杂运动的基础,通过分解复杂运动(如将曲线运动分解为直线分运动),可利用匀变速规律简化问题。
实际应用:
交通领域:计算汽车刹车距离(匀减速)、加速时间(匀加速)。
航天领域:分析火箭发射初期的匀加速阶段、卫星变轨时的加速度控制。
体育领域:投掷类项目(如铅球、标枪)的运动轨迹可近似为匀变速曲线运动(忽略空气阻力时)。
总结
“匀变速” 的核心是 “加速度恒定”,无论直线还是曲线运动,只要满足这一条件,就属于匀变速运动。理解这一概念有助于掌握物体速度变化的本质规律,是中学物理和大学力学的重要基础。